“蝴蝶效应”和“斯梅尔马蹄”
无规性的源泉在于初始条件的选择。一个动力系统的行为或运动轨道决定于两个因素。一个是系统的运动演化所遵从的规律,如牛顿定律;一个是系统的初始状态,即初始条件。经典力学指出,一个确定性系统在给定了运动方程后,它的轨道就唯一地取决于初始条件,一组初始值只有一条轨道,这就是系统行为对初值的依赖性。但是,任何测量都是有误差的,所以任何时候都不可能绝对精确地测定初始值。实验上给出的初值都只能是近似的。这个误差对系统的行为会不会有严重影响呢?经典力学断言,系统的行为或运动轨道对初值的依赖是不敏感的,知道了一个系统近似的初始条件,系统的行为就能够近似地计算出来。这就是说,从两组相接近的初值描绘出的两条轨道,会始终相互接近地在相空间里偕游并行,永远不会分道扬镳,泛泛的小影响不会积累起来形成一种大的效应。混沌研究却粉碎了传统科学中这种对近似性和运动的收敛性的信仰。处在混沌状态的系统,或者更一般地说对于一个非线性系统,运动轨道将敏感地依赖于初始条件。洛仑兹已经发现,从两组极相邻近的初始值出发的两条轨道,开始时似乎没有明显的偏离,但经过足够长的时间后,就会呈现出显著的差异来。这就是说,初值的微小差异,在运动过程中会逐渐被放大,终会导致运动轨道的巨大偏差,以至于这种偏差要多大就有多大。
在科学实验中,一种变化过程可能有一个临界点,在这一点上,一个微小的扰动可能被放大成一个重大的变化。而在混沌中,这种点无处不在,确定性系统初值的微小差异导致了系统整体的混沌后果。小的误差竟能带来巨大的灾难性后果,这一点早在1908年就被目光敏锐的庞加莱洞察到了。他在他的名著《科学与方法》中写道:我们觉察不到的极其轻微的原因决定着我们不能不看到的显著结果,于是我们说这个结果是由于偶然性。如果我们可以正确地了解自然定律以及宇宙在初始时刻的状态,那么我们就能够正确地预言这个宇宙在后继时刻的状态。不过,即使自然定律对我们已无秘密可言,我们也只能近似地知道初始状态。如果情况容许我们以同样的近似度预见后继的状态,这就是我们所要求的一切,那我们便说该现象被预言到了,它受规律支配。但是,情况并非总是如此;可以发生这样的情况:初始条件的微小差别在最后的现象中产生了极大的差别;前者的微小误差促成了后者的巨大误差。预言变得不可能了,我们有的是偶然发生的现象①。
这一段几乎是百年前的话,不正是我们近几十年才揭开的混沌来源之谜吗?洛仑兹从他关于长期天气预报的研究中悟出的正是这个道理。对于任何小块地区气候变化的误测,都会导致全球天气预报的迅速失真。不论气象观测站的网点如何密集,都不可能覆盖整个地球和从地面到高空的每一高度。在一尺之遥的空间范围内的一点气象涨落,都可能迅速波及到一尺之外、十尺之外、百尺之外的空间,小误差通过一系列湍流式的链锁反应,集结起来而成十倍、百倍、千倍地膨胀扩大,终于使天气预报变成一派胡言,在跨洋隔洲的地区形成山雨欲来风满楼的景象。洛仑兹非常形象地比喻说:巴西亚马孙河丛林里一只蝴蝶扇动了几下翅膀,三个月后在美国的得克萨斯州引起了一场龙卷风。人们把洛仑兹的比喻戏称为“蝴蝶效应”。这个看法当时并不为气象学家们所接受。
据说洛仑兹把“蝴蝶效应”说给他的一个朋友以说明长期天气预报不可能时,他的朋友回答说“预报不会成为问题”,“现在是要搞气象控制”。洛仑兹却不这样看,他认为,人工改变气候当然是可能的;但是当你这样做时,你就无法预测它会产生什么后果。简单的确定性系统如何会导致长期行为对初值的敏感依赖性呢?理解这一点的关键是要理解混沌的几何特性,即由系统内在的非线性相互作用在系统演化过程中所造成的“伸缩”与“折叠”变换。美国拓扑学家斯梅尔(Smale,Stephen 1930~)对此做出了重要贡献。斯梅尔是一个杰出的拓扑学家,本来在多维拓扑学的一些最奇特的问题上已经卓有成就。1958 年,他开始对动力系统的微分方程进行深入研究,并发表了一篇过于乐观的论文。他在这篇论文里提出了一个错误的猜想。他用极为严谨的数学语言论证说,一切动力系统最终都将进入一个并不十分奇异的行为;或者说,典型的动力学行为是定态的或周期的。虽然,一个动力系统可能会出现离奇古怪的性态,但斯梅尔认为这种性态不会是稳定的。
后来斯梅尔曾回忆说:“我的过分乐观引导我在那篇论文里认为,几乎所有常微分方程系统都是这样一些(结构稳定的)系统!”①他说如果他多少了解些庞加莱、伯克霍夫等人的文献,他就不会有那种愚蠢的思想。1959年圣诞节后,斯梅尔一家正在巴西首都里约热内卢暂住,他接到了他的朋友莱文松(Levinson,N.)的一封信,指出他的猜想是错误的,并告诉他自己关于受迫范德坡方程的研究已经提供了一个反例。早在本世纪20年代,德国物理学家范德坡(Van der Pol,B.)就已开始研究非线性电路的弛豫振荡问题,并得出了以他的名字命名的范德坡方程和受迫范德坡方程。1927年,范德坡又和范德马克(Van der Mark,J.)发现了著名的“分频”现象。莱文松用这个反例说明,一个系统既有混沌又有稳定性,混沌与稳定性共存;系统的这种奇特性质并不为小的扰动所破坏。当斯梅尔仔细研究了莱文松的文章,最后确信莱文松是对的时,他就把自己的猜想换成了另一个问题:典型的动力行为是什么?斯梅尔多年来是在拓扑学中进行探索的,他利用相空间对范德坡振子的全程可能性进行探索。
他注意的并不只是单条的轨线,而是全空间的性态;他的直觉由这系统的物理本质跃进到一种新型的几何本质。他思考的是形状在相空间中的拓扑变换,例如拉伸或压缩变换。这些变换有明确的物理意义。如系统中的耗散,由于摩擦而丧失能量,意味着系统在相空间中的形状将会收缩,甚至可能最终完全静止下来收缩到一点。为了反映范德坡振子的全部复杂运动性态,他想到相空间必须经历一种新的变换组合。这使他从观察振子的总体行为提出了一种几何模型——“斯梅尔马蹄”。斯梅尔马蹄的道理很简单。取一个正方形,把它拉伸为瘦长的矩形,再把它对折弯叠成马蹄形。然后想象把这马蹄嵌入一个新的矩形中,再重复相同的变换:挤压、折曲、拉伸……这实际上就像厨师揉面团的操作过程:首先是伸缩变换,使面团在一个方向擀平压薄,同时在另一个方向上伸长;然后是折叠变换,将拉长的两块面对折叠置。这种操作反复进行下去。可以设想,开始时先在面团上擦一层红颜色,那么在厨师揉面过程中,红色层将被拉长、变薄、交叠起来。经过多次反复操作后,原来相邻近的两个红色粒子会越来越远地分离开去,原来不相邻近的两个红色粒子却可能越来越靠近了。
斯梅尔马蹄映射模拟混沌折叠动力系统正是通过这两种变换而形成浑沌轨道几何图象的复杂性的。伸缩变换使相邻状态不断分离而造成轨道发散。但仅有伸缩变换还不足以扰乱相空间造成复杂性,还必须通过折叠变换。折叠是一种最强烈的非线性作用。伸缩和折叠的混合并不断反复,才可能产生动力系统相轨道的分离、汇合,产生无可预见的不规则运动。在混沌区内,相空间中的伸缩与折叠变换以不同的方式永不停息又永不重复地进行,从而造成了相轨道永不自交又永不相交的穿插盘绕、分离汇聚,完全“忘掉了”初始状态的一切信息,“丢弃了”未来与过去之间的一切联系,呈现出混沌运动。这就是系统长期行为对初值的敏感依赖性的源由。本来,斯梅尔企图只用拉伸与挤压去解释一切动力系统的行为,而不用会大大损害系统稳定性的折叠变换。但是折叠是必要的,因为折叠使动力系统的行为有动力性态上的根本变化,是导致混沌的一种重要作用。斯梅尔马蹄给数学家和物理学家提供了一个对动力系统运动的可能性的直观理解的几何图象。
在科学实验中,一种变化过程可能有一个临界点,在这一点上,一个微小的扰动可能被放大成一个重大的变化。而在混沌中,这种点无处不在,确定性系统初值的微小差异导致了系统整体的混沌后果。小的误差竟能带来巨大的灾难性后果,这一点早在1908年就被目光敏锐的庞加莱洞察到了。他在他的名著《科学与方法》中写道:我们觉察不到的极其轻微的原因决定着我们不能不看到的显著结果,于是我们说这个结果是由于偶然性。如果我们可以正确地了解自然定律以及宇宙在初始时刻的状态,那么我们就能够正确地预言这个宇宙在后继时刻的状态。不过,即使自然定律对我们已无秘密可言,我们也只能近似地知道初始状态。如果情况容许我们以同样的近似度预见后继的状态,这就是我们所要求的一切,那我们便说该现象被预言到了,它受规律支配。但是,情况并非总是如此;可以发生这样的情况:初始条件的微小差别在最后的现象中产生了极大的差别;前者的微小误差促成了后者的巨大误差。预言变得不可能了,我们有的是偶然发生的现象①。
这一段几乎是百年前的话,不正是我们近几十年才揭开的混沌来源之谜吗?洛仑兹从他关于长期天气预报的研究中悟出的正是这个道理。对于任何小块地区气候变化的误测,都会导致全球天气预报的迅速失真。不论气象观测站的网点如何密集,都不可能覆盖整个地球和从地面到高空的每一高度。在一尺之遥的空间范围内的一点气象涨落,都可能迅速波及到一尺之外、十尺之外、百尺之外的空间,小误差通过一系列湍流式的链锁反应,集结起来而成十倍、百倍、千倍地膨胀扩大,终于使天气预报变成一派胡言,在跨洋隔洲的地区形成山雨欲来风满楼的景象。洛仑兹非常形象地比喻说:巴西亚马孙河丛林里一只蝴蝶扇动了几下翅膀,三个月后在美国的得克萨斯州引起了一场龙卷风。人们把洛仑兹的比喻戏称为“蝴蝶效应”。这个看法当时并不为气象学家们所接受。
据说洛仑兹把“蝴蝶效应”说给他的一个朋友以说明长期天气预报不可能时,他的朋友回答说“预报不会成为问题”,“现在是要搞气象控制”。洛仑兹却不这样看,他认为,人工改变气候当然是可能的;但是当你这样做时,你就无法预测它会产生什么后果。简单的确定性系统如何会导致长期行为对初值的敏感依赖性呢?理解这一点的关键是要理解混沌的几何特性,即由系统内在的非线性相互作用在系统演化过程中所造成的“伸缩”与“折叠”变换。美国拓扑学家斯梅尔(Smale,Stephen 1930~)对此做出了重要贡献。斯梅尔是一个杰出的拓扑学家,本来在多维拓扑学的一些最奇特的问题上已经卓有成就。1958 年,他开始对动力系统的微分方程进行深入研究,并发表了一篇过于乐观的论文。他在这篇论文里提出了一个错误的猜想。他用极为严谨的数学语言论证说,一切动力系统最终都将进入一个并不十分奇异的行为;或者说,典型的动力学行为是定态的或周期的。虽然,一个动力系统可能会出现离奇古怪的性态,但斯梅尔认为这种性态不会是稳定的。
后来斯梅尔曾回忆说:“我的过分乐观引导我在那篇论文里认为,几乎所有常微分方程系统都是这样一些(结构稳定的)系统!”①他说如果他多少了解些庞加莱、伯克霍夫等人的文献,他就不会有那种愚蠢的思想。1959年圣诞节后,斯梅尔一家正在巴西首都里约热内卢暂住,他接到了他的朋友莱文松(Levinson,N.)的一封信,指出他的猜想是错误的,并告诉他自己关于受迫范德坡方程的研究已经提供了一个反例。早在本世纪20年代,德国物理学家范德坡(Van der Pol,B.)就已开始研究非线性电路的弛豫振荡问题,并得出了以他的名字命名的范德坡方程和受迫范德坡方程。1927年,范德坡又和范德马克(Van der Mark,J.)发现了著名的“分频”现象。莱文松用这个反例说明,一个系统既有混沌又有稳定性,混沌与稳定性共存;系统的这种奇特性质并不为小的扰动所破坏。当斯梅尔仔细研究了莱文松的文章,最后确信莱文松是对的时,他就把自己的猜想换成了另一个问题:典型的动力行为是什么?斯梅尔多年来是在拓扑学中进行探索的,他利用相空间对范德坡振子的全程可能性进行探索。
他注意的并不只是单条的轨线,而是全空间的性态;他的直觉由这系统的物理本质跃进到一种新型的几何本质。他思考的是形状在相空间中的拓扑变换,例如拉伸或压缩变换。这些变换有明确的物理意义。如系统中的耗散,由于摩擦而丧失能量,意味着系统在相空间中的形状将会收缩,甚至可能最终完全静止下来收缩到一点。为了反映范德坡振子的全部复杂运动性态,他想到相空间必须经历一种新的变换组合。这使他从观察振子的总体行为提出了一种几何模型——“斯梅尔马蹄”。斯梅尔马蹄的道理很简单。取一个正方形,把它拉伸为瘦长的矩形,再把它对折弯叠成马蹄形。然后想象把这马蹄嵌入一个新的矩形中,再重复相同的变换:挤压、折曲、拉伸……这实际上就像厨师揉面团的操作过程:首先是伸缩变换,使面团在一个方向擀平压薄,同时在另一个方向上伸长;然后是折叠变换,将拉长的两块面对折叠置。这种操作反复进行下去。可以设想,开始时先在面团上擦一层红颜色,那么在厨师揉面过程中,红色层将被拉长、变薄、交叠起来。经过多次反复操作后,原来相邻近的两个红色粒子会越来越远地分离开去,原来不相邻近的两个红色粒子却可能越来越靠近了。
斯梅尔马蹄映射模拟混沌折叠动力系统正是通过这两种变换而形成浑沌轨道几何图象的复杂性的。伸缩变换使相邻状态不断分离而造成轨道发散。但仅有伸缩变换还不足以扰乱相空间造成复杂性,还必须通过折叠变换。折叠是一种最强烈的非线性作用。伸缩和折叠的混合并不断反复,才可能产生动力系统相轨道的分离、汇合,产生无可预见的不规则运动。在混沌区内,相空间中的伸缩与折叠变换以不同的方式永不停息又永不重复地进行,从而造成了相轨道永不自交又永不相交的穿插盘绕、分离汇聚,完全“忘掉了”初始状态的一切信息,“丢弃了”未来与过去之间的一切联系,呈现出混沌运动。这就是系统长期行为对初值的敏感依赖性的源由。本来,斯梅尔企图只用拉伸与挤压去解释一切动力系统的行为,而不用会大大损害系统稳定性的折叠变换。但是折叠是必要的,因为折叠使动力系统的行为有动力性态上的根本变化,是导致混沌的一种重要作用。斯梅尔马蹄给数学家和物理学家提供了一个对动力系统运动的可能性的直观理解的几何图象。
教育新鲜事
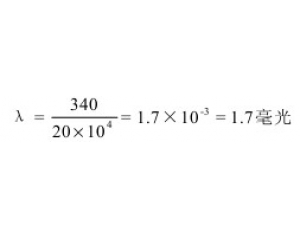 “超声“和“超音”
“超声“和“超音” 集市一瞥
集市一瞥 昆明湖上
昆明湖上 背道而驰
背道而驰