数学破题36计第34计 参数开门 宾主谦恭

第34计 参数开门 宾主谦恭?

●计名释义?

参数，顾名思义，是种“参考数”.供谁参考，供主变量参考.因此，参数对于主元，是种宾主关系，他为主元服务，受主元重用.?

在数学解题的过程中，反客为主，由参数唱主角戏的场景也异常精彩.?

有趣的是，“参数何在，选谁作参”的问题又成了解题破门的首要问题.此时，你有两种选择，一是参数就立足在面前，由你认定；二是参数根本不在，要你“无中生有”.??

●典例示范?

【例1】   P、Q、M、N四点都在椭圆x²+=1上，F为椭圆在y轴正半轴上的焦点，已知与共线，与共线，且·＝0，求四边形PMQN的面积的最小值和最大值.?

【分析】   四边形“没有”面积公式，因此难以用某边长为参数，建立面积函数式.?

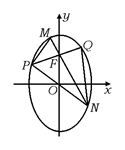幸好，它有两条互相垂直的对角线PQ和MN，使得四边形面积可用它们的乘积来表示，然而，它们要与已知椭圆找到关系，还需要一个参数k，并找到PQ，MN对k的依赖式.这就要“无中生有”了.?

【解答】   如图，由条件知MN和PQ

是椭圆的两条弦，相交于焦点F（0，1），

且PQ⊥MN，直线PQ、NM中至少有一条

存在斜率，不妨设PQ的斜率为k.?

【插语】   题设中没有这个k，

因此是“无中生有”式的参数.

我们其所以看中它，是认定它

不仅能表示|PQ|= f₁(k)，还能表示|MN|= f₂(k).?              例1题解图

【续解】   又PQ过点F（0，1），故PQ方程为y=kx+1，将此式代入椭圆方程得（2+k²)x²+2kx-1=0，设P、Q两点的坐标分别为（x₁，y₁)，(x₂，y₂)，则?

x₁=，?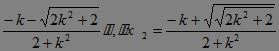

从而｜PQ｜²＝(x₁-x₂)²+(y₁-y₂)²=,?          亦即|PQ|=.?

【插语】   无论在椭圆方程中，还是P，Q，M，N的坐标中，x,y是当之无愧的主元.而这是新的函数关系|PQ|=f₁(k)=标志着主宾易位，问题已经发生了转程.?

【续解】   (ⅰ)当k≠0时，MN的斜率为-，同上可推得，

?｜MN｜=,?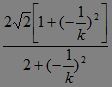

故四边形S＝|PQ|·|MN|=.?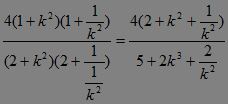

令u=k²+，得S=.?

因为u=k²+≥2，当k=±1时，u=2，S=，且S是以u为自变量的增函数，所以

≤S<2.?

【插语】   以上为本题解答的主干，以下k=0时情况，只是一个小小的补充，以显完善之美.其实，以“不失一般性”为由，设“k≠0”为代表解答亦可.这时，可省去下边的话.?

【续解】   (ⅱ)当k=0时，MN为椭圆长轴，｜MN｜＝2，|PQ|=，S=|PQ|·|MN|=2.

综合(ⅰ)(ⅱ)知，四边形PMQN面积的最大值为2，最小值为.?

【点评】   参数k将F(x，y)=0的方程转化为关于k的函数，达到“宾主融融”的和谐境界.参数成为解题化归中的一个重要的角色，有时在“反客为主”中成为主角.??

【例2】   对于a∈［-1,1］,求使不等式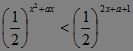恒成立的x的取值范围.?

【分析】   本题化指数不等式为整式不等式是不难的，问题是下一步应当怎样走！你是以x为主，讨论二次不等式？还是以a为主，讨论一次不等式？其难易之分是显而易见的.?

【解答】   y=为R上的减函数，∴由原不等式得：x²+ax>2x+a+1.?

即a(x-1)+(x²-2x-1)>0当a∈［-1，1］时恒成立.?

令f (a)=a(x-1)+(x²-2x-1).?

只须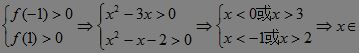(-∞,-1)∪(3,+∞)即为所求.【例3】   求函数y=的最大值与最小值.?

【解答一】   设tan=t，则y=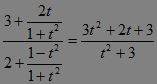

即t²(y-3)-2t+3y-3=0      ①?

∵t=tan∈R,?   ∴关于t的方程①必有实数根,?    ∴ Δ= 4-4·3(y-3)(y-1)≥0.?

即3y²-12y+8≤0，解得：2-≤y≤2+.

即y_max =2+，y_min =2-.?

【解答二】   原式变形：sin x-y cos x=2y-3，sin (x+φ)=2y-3.?

∵  |sin (x+φ)|≤1，∴≤|2y-3|.?

平方化简得：3y²-12y+8≤0.(下略)?

【点评】   本例中y是x的函数，而且是由三角函数与有理分式复合而成的函数,

按常法应是由自变量x的讨论确定函数的值域，可是本例的两种解法都是“反客为主”，或

通过转化为关于t的方程必有实数解，或通过正弦函数的有界性去直接处理函数的值域，理

由是:这样解法简单，而且同样能达到目的.??

【例4】   若cos²θ+2m sinθ-2m-2<0恒成立，试求实数m的取值范围.?

【解答】   反客为主，不看成关于sinθ的二次式，而看成关于m的一次式.?

原不等式即：2m(sinθ-1)<1+sin²θ,?

如sinθ=1，则0<1恒成立，此时m∈R.?

如sinθ≠1，∵sinθ∈［-1,1］，只能sinθ∈［-1,1)，于是sinθ-1<0.??

∴2m>2-

∵ (1-sinθ)+≥2.?

当且仅当1- sinθ=，即sinθ=1-时，=2,?

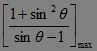∴??=2-2.?

为使2m>恒成立,只需2m>2-2，∴m>1-.?

综合得：所求m的取值范围为：m∈(1-，+∞).??

【例5】            已知动点P为双曲线=1的两个焦点，F₁，F₂的距离之和为定值，且cos∠F₁PF₂的最小值为.

(1)求动点P的轨迹方程；?

(2)若已知D(0,3)，M、N在动点P的轨迹上，且=λ，求实数λ的取值范围.?

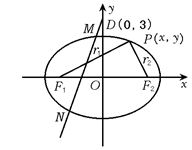【思考】   (1)动点的轨迹为椭圆，

当P在椭圆上时，由cos∠F₁PF₂=<0，

知∠F₁PF₂必为钝角且为最大角，

则P应为短轴端点(须证明),据此可

求出椭圆方程.?

(2)M、N在椭⊙上,?=λ时,

?与必共线,可用设参、消参                   例5题图

的方式确定λ的范围.?

【解答】   (1)设P(x,y)为轨迹上一点，命|PF₁|= r₁，|PF₂|= r₂，∵r₁+r₂=2a为定值，且

F₁(,0)，F₂(，0)为定点.?

∴点P的轨迹为椭圆，已知(cos∠F₁PF₂)_min=.?

而cos∠F₁PF₂=，这里>0，且r₁r₂≤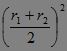=a²，∴≥，从而

cos∠F₁PF₂≥-1=1-,?

当且仅当r₁=r₂，即P为短轴端点时,1-=，∴a²=9，∵c²=5，∴b²=4.?

∴所求动点P的轨迹方程为：=1.?

(2)由(1)知点D(0,3)在椭圆外，设M(m，s)，N(n，t)在椭圆上.?

∵=λ，即(m，s-3)=λ(n，t-3),?

∴    ∴?

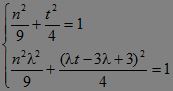消去n²得：??

化简得：(13λ-5)(λ-1)=6tλ(λ-1)?

如λ=1，则=，M，N重合于一点，且为椭圆与直线DM的切点.?

如λ≠1，有：t=，∵|t|≤2，-2≤≤2，解得λ∈［，5］.?

【点评】   设参、消参及参数的讨论，历来是高考的重点和难点之一，特别当参数较多时，往往感到不得要领或无从下手，对这类问题的基本对策是:当参数多于两个时，应逐渐消去非主要的参数，最终得到两个互相依存的参数，最后或通过均值不等式，或通过解一般不等式，或通过三角函数等数学手段去确定所求参数的范围.??

【小结】   什么样的问题适合“反客为主”？如果问题本身并不繁难，大可不必画蛇添足，故弄玄虚.如果问题本身虽然繁难，但题型单一，本来就无主次之分，也就无从反客为主.?

所以，适合“反客为主”的问题，一定是正面比较繁难，而交换主突位置（例如含参变量的方程或函数）则相对容易破解问题.??

●对应训练?

1.求使A=为整数的一切实数x.?

2.已知方程组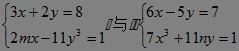同解，求m、n的值.?

3.解关于x的方程：x⁴-6x³-2(a-3)x²+2(3a+4)x+2a+a²=0.?

4.已知正项数列{a_n}中，a₁=1，且S_n=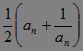，求该数列的通项.?

5.解方程x³+(1+)x²-2=0.??

●参考答案?

1.反客为主，让x为A服务.?

∵A-1=        当A∈Z时，亦有A-1∈Z.?

若x+1=0，则A=1∈Z(x= -1).?

若x+1≠0，有：A-1=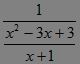∈Z.这有两种可能.?

(1)=±1.   x²-4x+2=0，x=2±；或x²-2x+4=0，无实数解，舍去.?

(2)是分子1的真分数.?           令x²-3x+3=1，得x=1或2.?

故所求实数为x=-1，1，2，2±.相应的整数为A=1，3，4，2.?

2.设两方程组的相同解为(x₀，y₀).?

由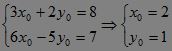

代入.?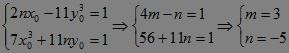

3.反客为主，原方程改写为关于a的一元二次方程：?

a²-(2x²-6x-2)a+x⁴-6x³+6x²+8x=0.?        ［a-(x²-3x-1)］² =(x-1)²?

a=(x²-3x-1)±(x-1)?

有x²-2x-2-a=0        ①?       或x²-4x-a=0         ②?

由①：（x-1）² = a+3.?

当a≥-3时，x=1±.?

由②：(x-2)²=a+4.?

当a≥-4时，x=2±.  故a<-4时，原方程无实根；?

a∈［-4,-3)时原方程有两解：x=2±；?a∈［-3，+∞)时，原方程有四解：

x=1±，x=2±.?

4.反客为主，先求S_n再求a_n，∵2S_n=(S _n - S_n-1)+，得：?

2S²_n - 2S_nS_n-1=S²_n-2S_nS_n-1+S²_n-1+1.?

∴S²_n - S²_n-1=1，∵a₁=S₁=1，令n=2，3，…，n，用叠加法可得S²_n - S²₁=n-1.?

∴S_n=,得a_n=S_n - S_n-1=，于是?a_n=.?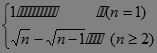

5.设a=，原方程转化为：a²-ax²-x(x²+x)=0，即(a-x²-x)(a+x)=0,?

∴x²+x=a或x= -a,?

∵a=.?

∴x²+x-=0x=±   或x=-.??