高考数学难点突破18不等式的证明策略

难点18  不等式的证明策略

不等式的证明，方法灵活多样，它可以和很多内容结合.高考解答题中，常渗透不等式证明的内容，纯不等式的证明，历来是高中数学中的一个难点，本难点着重培养考生数学式的变形能力，逻辑思维能力以及分析问题和解决问题的能力.

●难点磁场

(★★★★)已知a＞0，b＞0，且a+b=1.

求证：(a+)(b+)≥.

●案例探究

［例1］证明不等式(n∈N^*)

命题意图：本题是一道考查数学归纳法、不等式证明的综合性题目，考查学生观察能力、构造能力以及逻辑分析能力，属★★★★★级题目.

知识依托：本题是一个与自然数n有关的命题，首先想到应用数学归纳法，另外还涉及不等式证明中的放缩法、构造法等.

错解分析：此题易出现下列放缩错误：

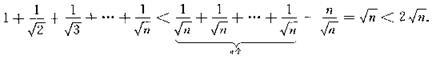
这样只注重形式的统一，而忽略大小关系的错误也是经常发生的.

技巧与方法：本题证法一采用数学归纳法从n=k到n=k+1的过渡采用了放缩法；证法二先放缩，后裂项，有的放矢，直达目标；而证法三运用函数思想，借助单调性，独具匠心，发人深省.

证法一：(1)当n等于1时，不等式左端等于1，右端等于2，所以不等式成立；

(2)假设n=k(k≥1)时，不等式成立，即1+＜2，

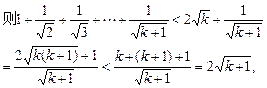
∴当n=k+1时，不等式成立.

综合(1)、(2)得：当n∈N^*时，都有1+＜2.

另从k到k+1时的证明还有下列证法：

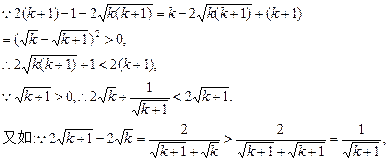
证法二：对任意k∈N^*，都有：

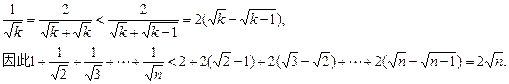
证法三：设f(n)= 

那么对任意k∈N?^* 都有：

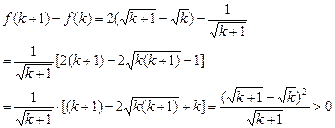
∴f(k+1)＞f(k)

因此，对任意n∈N^* 都有f(n)＞f(n－1)＞…＞f(1)=1＞0，

∴

［例2］求使≤a(x＞0，y＞0)恒成立的a的最小值.

命题意图：本题考查不等式证明、求最值函数思想、以及学生逻辑分析能力，属于★★★★★级题目.

知识依托：该题实质是给定条件求最值的题目，所求a的最值蕴含于恒成立的不等式中，因此需利用不等式的有关性质把a呈现出来，等价转化的思想是解决题目的突破口，然后再利用函数思想和重要不等式等求得最值.

错解分析：本题解法三利用三角换元后确定a的取值范围，此时我们习惯是将x、y与cosθ、sinθ来对应进行换元，即令=cosθ，=sinθ(0＜θ＜)，这样也得a≥sinθ+cosθ，但是这种换元是错误的.其原因是：(1)缩小了x、y的范围；(2)这样换元相当于本题又增加了“x、y=1”这样一个条件，显然这是不对的.

技巧与方法：除了解法一经常用的重要不等式外，解法二的方法也很典型，即若参数a满足不等关系，a≥f(x)，则a_min=f(x)_max；若 a≤f(x)，则a_max=f(x)_min，利用这一基本事实，可以较轻松地解决这一类不等式中所含参数的值域问题.还有三角换元法求最值用的恰当好处，可以把原问题转化.

解法一：由于a的值为正数，将已知不等式两边平方，得：

x+y+2≤a²(x+y)，即2≤(a²－1)(x+y)，                                                     ①

∴x，y＞0，∴x+y≥2，                                                                                  ②

当且仅当x=y时，②中有等号成立.

比较①、②得a的最小值满足a²－1=1，

∴a²=2，a= (因a＞0)，∴a的最小值是.

解法二：设.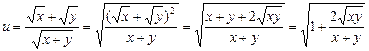

∵x＞0，y＞0，∴x+y≥2 (当x=y时“=”成立)，

∴≤1，的最大值是1.

从而可知，u的最大值为，

又由已知，得a≥u，∴a的最小值为.

解法三：∵y＞0，

∴原不等式可化为+1≤a，

设=tanθ，θ∈(0，).

∴tanθ+1≤a；即tanθ+1≤asecθ

∴a≥sinθ+cosθ=sin(θ+)，                                                                        ③

又∵sin(θ+)的最大值为1(此时θ=).

由③式可知a的最小值为.

●锦囊妙计

1.不等式证明常用的方法有：比较法、综合法和分析法，它们是证明不等式的最基本的方法.

(1)比较法证不等式有作差(商)、变形、判断三个步骤，变形的主要方向是因式分解、配方，判断过程必须详细叙述；如果作差以后的式子可以整理为关于某一个变量的二次式，则考虑用判别式法证.

(2)综合法是由因导果，而分析法是执果索因，两法相互转换，互相渗透，互为前提，充分运用这一辩证关系，可以增加解题思路，开扩视野.

2.不等式证明还有一些常用的方法：换元法、放缩法、反证法、函数单调性法、判别式法、数形结合法等.换元法主要有三角代换，均值代换两种，在应用换元法时，要注意代换的等价性.放缩性是不等式证明中最重要的变形方法之一，放缩要有的放矢，目标可以从要证的结论中考查.有些不等式，从正面证如果不易说清楚，可以考虑反证法.凡是含有“至少”“惟一”或含有其他否定词的命题，适宜用反证法.

证明不等式时，要依据题设、题目的特点和内在联系，选择适当的证明方法，要熟悉各种证法中的推理思维，并掌握相应的步骤、技巧和语言特点.

●歼灭难点训练

一、填空题

1.(★★★★★)已知x、y是正变数，a、b是正常数，且=1，x+y的最小值为__________.

2.(★★★★)设正数a、b、c、d满足a+d=b+c，且|a－d|＜|b－c|，则ad与bc的大小关系是__________.

3.(★★★★)若m＜n，p＜q，且(p－m)(p－n)＜0，(q－m)(q－n)＜0，则m、n、p、q的大小顺序是__________.

二、解答题

4.(★★★★★)已知a，b，c为正实数，a+b+c=1.

求证：(1)a²+b²+c²≥

 (2)≤6

5.(★★★★★)已知x，y，z∈R，且x+y+z=1，x²+y²+z²=，证明：x，y，z∈［0，］

6.(★★★★★)证明下列不等式：

(1)若x，y，z∈R，a，b，c∈R⁺，则z²≥2(xy+yz+zx)

(2)若x，y，z∈R⁺，且x+y+z=xyz，

则≥2()

7.(★★★★★)已知i，m、n是正整数，且1＜i≤m＜n.

(1)证明：nⁱA＜mⁱA；

(2)证明：(1+m)ⁿ＞(1+n)^m

8.(★★★★★)若a＞0，b＞0，a³+b³=2，求证：a+b≤2，ab≤1.

参考答案

难点磁场

证法一：(分析综合法）

欲证原式，即证4(ab)²+4(a²+b²)－25ab+4≥0，即证4(ab)²－33(ab)+8≥0，即证ab≤或ab≥8.

∵a＞0，b＞0，a+b=1，∴ab≥8不可能成立

∵1=a+b≥2，∴ab≤，从而得证.

证法二：(均值代换法)

设a=+t₁，b=+t₂.

∵a+b=1，a＞0，b＞0，∴t₁+t₂=0，|t₁|＜，|t₂|＜

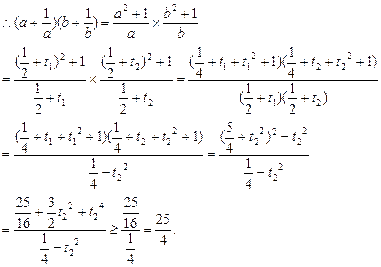
显然当且仅当t=0，即a=b=时，等号成立.

证法三：(比较法）

∵a+b=1，a＞0，b＞0，∴a+b≥2，∴ab≤

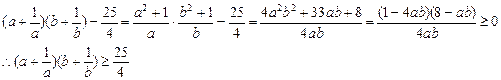
证法四：(综合法)

∵a+b=1， a＞0，b＞0，∴a+b≥2，∴ab≤.

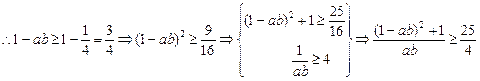
证法五：(三角代换法）

∵ a＞0，b＞0，a+b=1，故令a=sin²α，b=cos²α，α∈(0，)

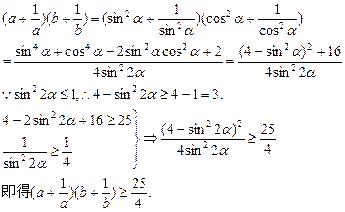2

歼灭难点训练

一、1.解析：令=cos²θ，=sin²θ，则x=asec²θ，y=bcsc²θ，∴x+y=asec²θ+bcsc²θ=a+b+atan²θ+bcot²θ≥a+b+2.

答案：a+b+2

2.解析：由0≤|a－d|＜|b－c|(a－d)²＜(b－c)²(a+b)²－4ad＜(b+c)²－4bc?

∵a+d=b+c，∴－4ad＜－4bc，故ad＞bc.

答案：ad＞bc

3.解析：把p、q看成变量，则m＜p＜n，m＜q＜n.

答案：m＜p＜q＜n

二、4.(1)证法一：a²+b²+c²－=(3a²+3b²+3c²－1)

=［3a²+3b²+3c²－(a+b+c)²］

=［3a²+3b²+3c²－a²－b²－c²－2ab－2ac－2bc］

=［(a－b)²+(b－c)²+(c－a)²］≥0  ∴a²+b²+c²≥

证法二：∵(a+b+c)²=a²+b²+c²+2ab+2ac+2bc≤a²+b²+c²+a²+b²+a²+c²+b²+c²

∴3(a²+b²+c²)≥(a+b+c)²=1  ∴a²+b²+c²≥

证法三：∵∴a²+b²+c²≥

∴a²+b²+c²≥

证法四：设a=+α，b=+β，c=+γ.

∵a+b+c=1，∴α+β+γ=0

∴a²+b²+c²=(+α)²+(+β)²+(+γ)²

=+ (α+β+γ)+α²+β²+γ²

=+α²+β²+γ²≥

∴a²+b²+c²≥

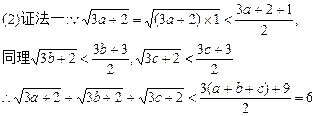
∴原不等式成立.

证法二：

∴≤＜6

∴原不等式成立.

5.证法一：由x+y+z=1，x²+y²+z²=，得x²+y²+(1－x－y)²=，整理成关于y的一元二次方程得：

2y²－2(1－x)y+2x²－2x+=0，∵y∈R，故Δ≥0

∴4(1－x)²－4×2(2x²－2x+)≥0，得0≤x≤，∴x∈［0，］

同理可得y，z∈［0，］

证法二：设x=+x′，y=+y′，z=+z′，则x′+y′+z′=0，

于是=(+x′)²+(+y′)²+(+z′)²

=+x′²+y′²+z′²+ (x′+y′+z′)

=+x′²+y′²+z′²≥+x′²+=+x′²

故x′²≤，x′∈［－，］，x∈［0，］，同理y，z∈［0，］

证法三：设x、y、z三数中若有负数，不妨设x＜0，则x²＞0，=x²+y²+z²≥x²+＞，矛盾.

x、y、z三数中若有最大者大于，不妨设x＞，则=x²+y²+z²≥x²+=x²+=x²－x+

=x(x－)+＞；矛盾.

故x、y、z∈［0，］

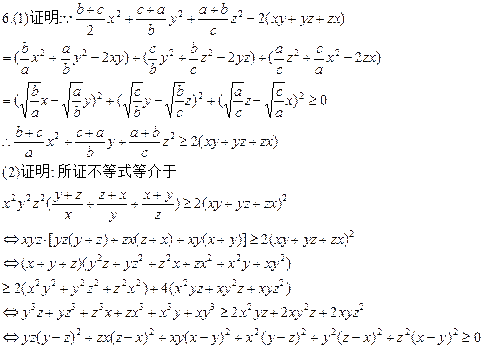
∵上式显然成立，∴原不等式得证.

7.证明：(1)对于1＜i≤m，且A =m·…·(m－i+1)，

，

由于m＜n，对于整数k=1，2，…，i－1，有，

所以

(2)由二项式定理有：

(1+m)ⁿ=1+Cm+Cm²+…+Cmⁿ，

(1+n)^m=1+Cn+Cn²+…+Cn^m，

由(1)知mⁱA＞nⁱA (1＜i≤m，而C=

∴mⁱCⁱ_n＞nⁱCⁱ_m(1＜m＜n

∴m⁰C=n⁰C=1，mC=nC=m·n，m²C＞n²C，…，

m^mC＞n^mC，m^m+1C＞0，…，mⁿC＞0，

∴1+Cm+Cm²+…+Cmⁿ＞1+Cn+C²_mn²+…+Cn^m，

即(1+m)ⁿ＞(1+n)^m成立.

8.证法一：因a＞0，b＞0，a³+b³=2，所以

(a+b)³－2³=a³+b³+3a²b+3ab²－8=3a²b+3ab²－6

=3［ab(a+b)－2］=3［ab(a+b)－(a³+b³)］=－3(a+b)(a－b)²≤0.

即(a+b)³≤2³，又a+b＞0，所以a+b≤2，因为2≤a+b≤2，

所以ab≤1.

证法二：设a、b为方程x²－mx+n=0的两根，则，

因为a＞0，b＞0，所以m＞0，n＞0，且Δ=m²－4n≥0                                         ①

因为2=a³+b³=(a+b)(a²－ab+b²)=(a+b)［(a+b)²－3ab］=m(m²－3n)

所以n=                                                                                                    ②

将②代入①得m²－4()≥0，

即≥0，所以－m³+8≥0，即m≤2，所以a+b≤2，

由2≥m 得4≥m²，又m²≥4n，所以4≥4n，

即n≤1，所以ab≤1.

证法三：因a＞0，b＞0，a³+b³=2，所以

2=a³+b³=(a+b)(a²+b²－ab)≥(a+b)(2ab－ab)=ab(a+b)

于是有6≥3ab(a+b)，从而8≥3ab(a+b)+2=3a²b+3ab²+a³+b³=?

(a+b)³，所以a+b≤2，(下略）

证法四：因为

≥0，

所以对任意非负实数a、b，有≥

因为a＞0，b＞0，a³+b³=2，所以1=≥，

∴≤1，即a+b≤2，(以下略）

证法五：假设a+b＞2，则

a³+b³=(a+b)(a²－ab+b²)=(a+b)［(a+b)²－3ab］＞(a+b)ab＞2ab，所以ab＜1，

又a³+b³=(a+b)［a²－ab+b²］=(a+b)［(a+b)²－3ab］＞2(2²－3ab)

因为a³+b³=2，所以2＞2(4－3ab)，因此ab＞1，前后矛盾，故a+b≤2(以下略)