【揭秘】走出含参变量的线性规划问题的解题陷阱
线性规划是沟通代数与几何的桥梁，是数形结合思想的集中体现．传统的线性规划问题主要研究的是在线性或非线性约束条件下求解目标函数的最值，就知识本身而言并不是难点．但是，近年来这类问题的命题设置在能力立意的命题思想指导下出现了新的动向：一方面将它与函数、方程、不等式、数列、平面向量、解析几何等知识交汇在一起；另一方面在这些问题背景中引进参变量，变换设问角度，提高思维强度，增加题目难度．下面我们对线性规划中参变量的新情景设置给出深度分析，帮助同学们走出思维误区，正确求解线性规划问题．
一、约束条件中设置的参变量 不等式组中含有参变量是线性规划命题的新动向之一，由于不能明确可行域的形状，因此增加了解题时画图分析的难度．求解这类问题时要有全局观念，结合目标函数逆向分析题意，整体把握解题的方向．
1 制约可行域的形状
本题特点是题设条件所给的区域边界为三“静”一“动”，画出符合题意条件的可行域图形是解题的关键．解题时可先画出“静”的三个条件给出的三角形形状，再画出变化“动”直线x+my+n=0，此时容易出现两种问题：一是如何使图形为直角三角形，二是怎样满足其面积为四分之五．解题时应先定形，即先得出直角三角形；再定量，即再求解使直角三角形面积为四分之五时，参数n的值．
2 制约目标函数的最值
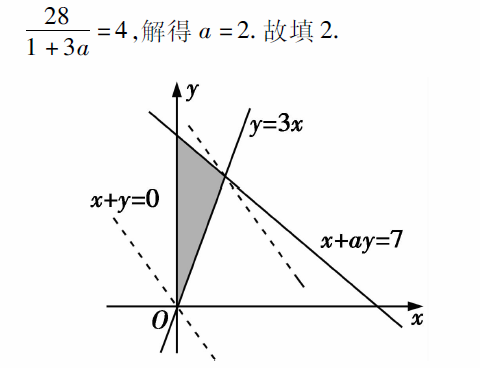
线性规划问题中，目标函数的最值一般都会在可行域图形的顶点处取得，对应着两条相交直线的交点．本题中易错之处是没有注意到题设条件a>1，得不到直线x+ay=7的斜率大于－1的转换，从而找不到最大值该在哪两条直线的交点处取得．
3 制约目标结构式的形式
解决本题的关键是找到平面区域D?n内的整点的个数的组成规律，从而得出a?n的表达式．而制约区域D?n内的整点个数的因素是条件不等式组中y≤－n(x－3)的参数n的取值．本题的易错点是不知道从特值n=1，n=2开始研究，找到其中隐含的规律，而这种方法恰好是求解有数列背景的线性规划问题的基本方法．
二、目标式中设置的参变量 目标函数中设置参变量是线性规划命题的又一种新动向，旨在增加探索问题的动态性和开放性，考查考生的探究性思维能力．从目标函数的结论入手，对图形的动态分析和对变化过程中的相关量的准确定位是求解这类问题的主要思维方法
1 求解目标式中的参数值
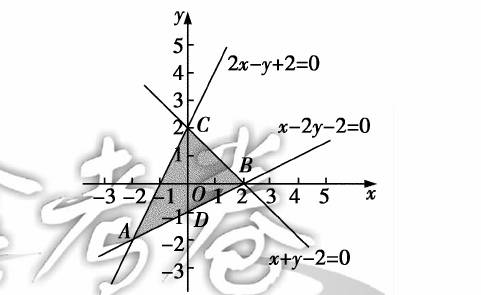
目标函数的最优解不唯一的问题，往往是指目标函数取得最值时所表示的直线与可行域中的一条直线重合．据此，求解这类问题的方法可以让目标函数所表示的直线与可行域中的每条边界直线重合，从而求解．利用这种方法求解时，切记要进行检验，区分何时取得最大值的最优解不唯一，何时取得最小值的最优解不唯一，不能出错．
2 探究目标式中的参数范围
解题时先转化目标中的向量关系，使其对应一个二元目标函数，然后再利用可行域的条件求出目标函数的最大值和最小值，从而得到不等式恒成立时实数m的取值范围．
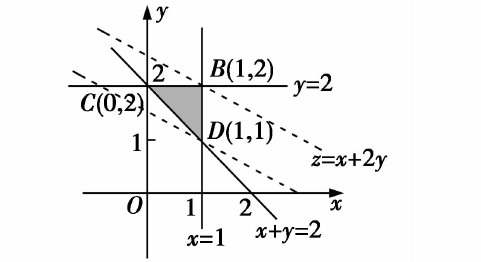
目标函数以向量的形式出现是一种新的创意，本题易错点是面对目标中的向量关系不知道如何转化．求解线性规划问题的基本形式是探究二元目标函数的最值，因此转化向量关系的主要思路和基本目标就是找到其中对应的二元目标函数，然后结合可行域求解最值．
2 计算目标式中条件的最值
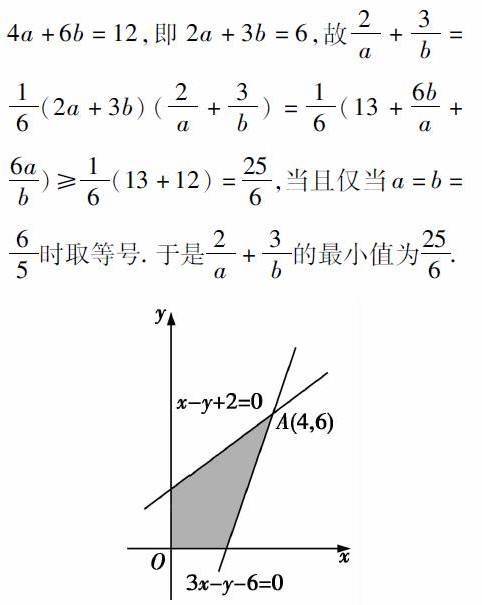
高考中的线性规划问题，既继承了传统的由二元不等式组构成条件，探究二元目标函数最值的基本形式，同时还赋予了创新的命题形式．变更题设条件或目标式中的线性关系为非线性关系，同时渗透参变量的命题风格，增加了可行域条件的动态变化方式，转化了目标函数的探求类型，提升了对问题探究的能力要求，这就要求同学们在面对这些全新的问题时要与时俱进地进行创新分析，增加应变智慧，才能提升我们的解题能力．
相关文章
平凉：职业教育搭平台
习总书记关切事丨这一年
国外创投新闻 印度教育推荐内容
学习方法