对欧氏几何的挑战—非欧几何
欧几里得的《几何原本》第一卷中提出23个定义、5个公理、5个公设。麻烦都出在第五公设,也就是平行公设上。《原本》的平行公设是这么叙述的:平面上两直线被一直线所截,如果截线一侧的两内角之和小于两直角,则此二直线必相交于截线的这一侧。欧几里得的第23个定义是平行线,它们必须在同一平面上,并且两边无限延长后均不相交。这个公设不像其它公理公设在直观上明显,而且直到命题29才需用第五公设来证明。因此,从古到今激起许多人企图利用其他公理和公设来证明这个平行公设。长期以来,这种“证明”并未取得成功,但是,却大大简化了第五公设,使得它变成直观上明显的等价命题。其中最常用的是苏格兰物理学家、数学家普雷范尔的命题:过不在给定直线上的一点,可做一条且仅可做一条直线与该给定直线平行。
他在1795年证明这命题与平行公设等价之后,成为平行公设的通用提法。实际上,公元五世纪普洛克洛斯已经提到过。沿着这条路走下去得出一些与平行公设等价的命题:(1)任一三角形的内角之和等于两直角,后来这命题可简化为(1),至少存在一个三角形,其三个角之和等于两直角。(2)存在一对相似三角形但不全等。(3)过任意不共线的三点可以做一圆。(4)在小于60°的角内一点,总可以做一直线与该角两边相交。(5)两条相交直线不能同时平行于第三条直线。这些命题也都同平行公设一样不能单独从其他几条公理中推出,如果推出,必定都隐含运用一条等价的公理,这样一种办法行不通。于是许多人采取第二种办法:即用平行公设相矛盾的命题代替平行公设,即①罗氏公设,过一直线外一点可作两条直线与该直线平行;②黎氏公设,过一直线外一点不能作直线与该直线平行,并试图推出矛盾但没有成功,而导致非欧几何学的成立。
他在1795年证明这命题与平行公设等价之后,成为平行公设的通用提法。实际上,公元五世纪普洛克洛斯已经提到过。沿着这条路走下去得出一些与平行公设等价的命题:(1)任一三角形的内角之和等于两直角,后来这命题可简化为(1),至少存在一个三角形,其三个角之和等于两直角。(2)存在一对相似三角形但不全等。(3)过任意不共线的三点可以做一圆。(4)在小于60°的角内一点,总可以做一直线与该角两边相交。(5)两条相交直线不能同时平行于第三条直线。这些命题也都同平行公设一样不能单独从其他几条公理中推出,如果推出,必定都隐含运用一条等价的公理,这样一种办法行不通。于是许多人采取第二种办法:即用平行公设相矛盾的命题代替平行公设,即①罗氏公设,过一直线外一点可作两条直线与该直线平行;②黎氏公设,过一直线外一点不能作直线与该直线平行,并试图推出矛盾但没有成功,而导致非欧几何学的成立。
教育新鲜事
 数学经典问题-抽屉原理
数学经典问题-抽屉原理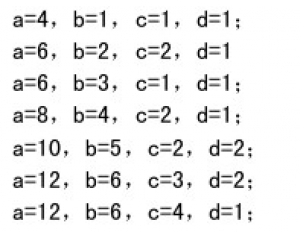 分马
分马 龟鹤算
龟鹤算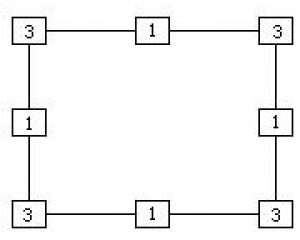 藏盗法
藏盗法