为什么高中数学开篇就是“集合与逻辑”这一章？不仅仅是因为我们要用集合去表示求解的结果，更因为这一部分是整个高中数学学习的思维基础。

集合解决的是什么问题？

我们知道集合里的元素有三个特性：确定性、互异性和无序性。所以集合虽然包罗万象，却还是有很多东西不是集合，因为没有一个确定的边界。数学关心的是精确的表述。

集合用来描述事物的性质。我们常常说一个东西是怎样怎样的，从数学的角度看就是在说这个事物属于一个什么什么集合。比如“985高校”表示了一批大学的集合。

集合的使用，就是从特殊抽象出一般。一个集合包括了一些元素，也就意味着这些元素具有这个集合所表示的某种共性。

所以集合解决的是“是怎样”的问题。

命题又是什么呢？

命题是判断一件事情的语句。它必须能够确定真假。

最常见的命题形式是“条件—结论”，也即“如果p，则q”的形式，p和q是两个语句。

命题解决的是“是不是”的问题。

集合和命题为什么放在一块学？

因为“是不是”的问题本质上也是“是怎样”的问题。就像在考试中“判断题”只是题型的一种，但其实所有其他的题型都可以转化为判断题的形式给出。

我们演示一下集合和命题的这种对应关系。

如果p，则q。

或者说p能推出q。

如果条件p可以写为集合A的形式，结论q可以写为集合B的形式，条件和结论所描述的对象都是事物x，那么这个命题就可以表述为

如果x属于A，则x属于B。

这和“A的所有元素都属于B”是一个意思。

从集合的知识我们知道，这意味A是B的子集。

从充分必要关系来说，这意味着p是q的充分条件（q是p的必要条件）。

从语言上理解“充分”和“必要”：

p能推出q，p成立就有q成立，即p成立对于q成立来说是足够的（充分的）；

同时p成立必然要有q成立，所以q成立对于p成立来说是必要的。

如果q也能推出p，

即“如果x属于B，则x属于A。”那么B的所有元素都属于A，

意味着q是p的充分条件（p是q的充分条件）。合起来p和q互为充要条件。

从集合上看，A的所有元素都属于B，B的所有元素都属于A，意味着A = B，两个集合相等。

如果p能推出q，q不能推出p，

即“如果x属于B，x未必属于A。”也即B中至少有一个元素x不属于A，则A是B的一个真子集。

这种情况下p是q的充分不必要条件（q是p的必要不充分条件）。

或者说p和q是等价的。所以如果两个命题的真假性一致，它们就是等价的。从这里发散一下思维，可以对“等价转化”的数学思想有更深的理解。

逆否命题用集合来理解

“如果x属于A，则x属于B。”前面说了这意味着A是B的子集，作出韦恩图如下。

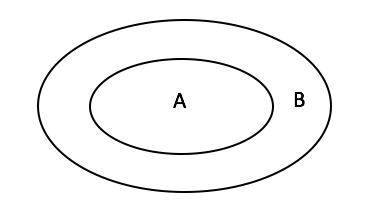
从上图显然看出，如果原命题为真，它的逆否命题“如果x不属于B，则x不属于A”也是真的。同时可推出如果原命题为假，它的逆否命题必为假。（因为逆否关系是相互的。）

即原命题和其逆否命题是等价的。

全称、特称命题的否命题用集合来理解

全称命题说的是“任意x属于A，则x属于B。” 这还是意味着A是B的子集。

它的否定的韦恩图包括以下几种情形。

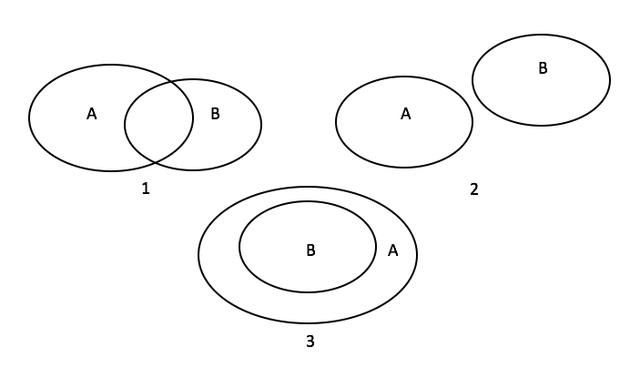
上述三种情形都包括在否命题“存在x属于A，不属于B”里。而“任意x属于A，不属于B”只是情形2。

所以全称命题的否定是特称命题。因为否定的关系也是相互的，所以同时可知特称命题的否定是全称命题。